【转载】关于动画，你需要知道的_Animation, Web动画教程

作者：大漠日期：2016-05-28 点击：5511

特别声明，本文转载于@十年踪迹的《关于动画，你需要知道的》,如果需要转载，烦请注明文章出处：https://www.h5jun.com/post/animations-you-should-know.html

这是我今年为新人设计的一门课程的文字精简版，完整的PPT可参考:

简单的 JS 动画

在浏览器里，动画实现的基本原理非常简单明了，其实就是采用定时器改变显示元素的一些属性的过程。不管是 JavaScript 操作 DOM 的动画，还是 CSS3 动画，还是 Canvas 动画，或者 SVG 动画，区别只是使用的 API、何种定时器，影响什么环境（DOM/Canvas/SVG/WebGL）。

var deg = 0;
block.addEventListener("click", function(){
  var self = this;
  requestAnimationFrame(function change(){
    self.style.transform = "rotate(" + (deg++) +"deg)";
    requestAnimationFrame(change);
  });
});

上面的例子里，我们使用了定时器 requestAnimationFrame，requestAnimationFrame 是浏览器专为渲染刷新设计的定时器接口，在早期版本的浏览器里，我们可以用 setTimeout或者setInterval来代替它。定时器改变了方块元素的角度，每一次定时器触发我们就刷新并增加一次它的角度值，这样就产生了方块不断旋转的动态效果。

这就是我们需要的动画，几行原生JS代码就够了，是不是很简单呢？

事实上，上面的动画不是最佳的实现方法。它存在着几个明显的改进点。

简单动画的问题

首先，requestAnimationFrame（或者 setTimeout、setInterval 等其他定时器）并不能保证严格在某个时间点被触发。还记得 JavaScript 的单线程非阻塞模型吧？如果 requestAnimationFrame 被其他任务给阻塞了，那么动画就会变慢:

var deg = 0;
block.addEventListener("click", function(){
  setInterval(function(){
    var i = 0;  
    var t = Date.now();
    while(++i < 200000000); //模拟耗时操作
    console.log(Date.now() - t);
  }, 100);

  var self = this;
  requestAnimationFrame(function change(){
    self.style.transform = "rotate(" + (deg++) +"deg)";
    requestAnimationFrame(change);
  });
});

上面的动画，因为有其他的定时器耗时的操作，导致动画变慢。

其次，一个更加麻烦的问题是，上面的动画我们通过定时器给旋转角度增量的方式，或者说得更泛一点（暂时忽略前面那个定时器触发时间不确定的问题），我们通过定义速度的方式来改变动画，这会导致我们很难精确控制动画时间和动画的幅度。像前面这种匀速运动其实还好，如果做一些复杂的变速运动，按照我们的定义方式，我们本该设置的元素属性值将会类似于求积分，然而时间又不连贯。

var x = 0, y = 0;
block.addEventListener("click", function(){
  var self = this;
  requestAnimationFrame(function change(){
    self.style.transform = "translate(" + 
      (x++) + "px," + 100 * Math.cos(Math.PI * (y++/180)) + "px)";
    requestAnimationFrame(change);
  });
});

上面的动画由于时间不连贯绘制出来的曲线只能近似等于正弦曲线。

动画是“位移”关于“时间”的函数

动画，是位移关于时间的函数：$$s = f(t)$$

所以，我们不该采用增量的方式来执行动画，为了更精确地控制动画，更合适的方式是将动画与时间联系起来：

动画与时间关联

function startAnimation(){
  var startTime = Date.now();

  requestAnimationFrame(function change(){
    var current = Date.now() - startTime;

    console.log("动画已执行时间: %fms", current);

    requestAnimationFrame(change);
  });
}

动画通常情况下有终止时间，如果是循环动画，我们也可以看做特殊的——当动画达到终止时间之后，重新开始动画。因此，我们可以将动画时间归一(Normalize)表示：

动画时间归一化表示

function startAnimation(duration, isLoop){
  var startTime = Date.now();

  requestAnimationFrame(function change(){
    var p = (Date.now() - startTime) / duration;

    if(p >= 1.0){
      if(isLoop){
        startTime += duration;
        p -= 1.0;
      }else{
        p = 1.0;
      }
    }

    console.log("动画已执行进度: %f", p);
    if(p < 1.0){
      requestAnimationFrame(change);
    }
  });
}

我们可以用时间来控制动画：

用时间来控制动画周期精确在1秒

让滑块在2秒内向右匀速移动200px

我们可以将通过时间控制动画与前面的简单增量的办法做一个对比：

	时间	增量
幅度控制	√	√
时间控制	√	X
幅度控制	√	√
不延迟	√	X
不掉帧	X	√

变速运动

变速运动可以模拟一些物理效果、曲线运动，以及其他的一些非均匀变化的特效。

匀加速运动

加速度恒定，速度从0开始随时间增加而均匀增加。

$$t = T \cdot p$$

$$s_t = S \cdot p ^ {2} = (\frac{S}{T^2}) t^2$$

$$v = \frac{2S}{T^2} \cdot t = \frac{2Sp}{T}$$

$$a = \frac{2S}{T^2}$$

通过推导可以得到匀减速运动的位移时间公式：$$s_t = S \cdot p ^ {2}$$

匀速、匀加速运动对比

匀减速运动

实现“刹车”效果，速度随时间均匀减小直到0，让物体停止运动。

$$t = T \cdot p$$

$$s_t = \frac{2S}{T} \cdot t - (\frac{S}{T^2}) t^2 = Sp(2-p)$$

$$v = \frac{2S(1-p)}{T} = \frac{2S}{T} - \frac{2S}{T^2} \cdot t$$

$$a = - \frac{2S}{T^2} $$

通过推导可以得到匀减速运动的位移时间公式：$$s_t = Sp(2-p)$$

运动的组合

平面上的运动

让x、y轴同时分别运动，可以让物体沿平面轨迹运动。

抛物线运动

抛物线运动 x 轴做匀速直线运动，y 轴做匀加速直线运动

正弦线运动

正弦线运动 x 轴做匀速直线运动，y 轴的运动是时间 t 的正弦函数。

圆周运动

代数方程 $$x^2 + y^2 = r^2$$

参数方程

$$x = R \cdot cos(ωt) $$

$$y = R \cdot sin(ωt) $$

极坐标方程

$$ρ = R$$

圆的代数方程涉及到开根号后的正负号问题，因此一般不使用。

圆周运动 - 参数方程

根据参数方程，圆周运动 x 轴是时间 t 的余弦函数， y 轴是时间 t 的正弦函数。

圆周运动 - 极坐标方程

根据极坐标方程，圆周运动的旋转角度是时间 t 的线性函数。

动画算子： easing

我们总结一下上面的各类动画，发现它们是非常相似的，匀速运动、匀加速运动、匀减速运动、圆周运动唯一的区别仅仅在于位移方程：

匀速运动：$$s_p = S \cdot P$$

匀加速运动：$$s_p = S \cdot P^2$$

匀减速运动：$$s_p = S \cdot P \cdot (2 - P)$$

圆周运动x轴：$$s_p = S \cdot cos(ωt)$$

圆周运动y轴：$$s_p = S \cdot sin(ωt)$$

我们把共同的部分 S 去掉，得到一个关于 p 的方程 $$e_p = E(p)$$ ，这个方程我们称为动画的算子(easing)，它决定了动画的性质。

匀速算子：$$e_p = P$$

匀加速算子：$$e_p = P^2$$

匀减速算子：$$e_p = P \cdot (2 - P)$$

圆周算子x轴：$$e_p = cos(ωt)$$

圆周算子y轴：$$e_p = sin(ωt)$$

动画的简易封装

为了实现更加复杂的动画，我们可以将动画进行简易的封装，要进行封装，我们先要抽象出动画相关的要素：

动画时长：$$T = duration$$

动画进程：$$ p = \frac{t}{T}(p \in [0, 1])$$

easing：$$e = f(p)$$

动画方程：$$[x, y] = G(e) = G(f(p))$$

动画生命周期：开始、进行中、结束。

动画的简易封装

function Animator(duration, progress, easing){
  this.duration = duration;
  this.progress = progress;
  this.easing = easing || function(p){return p};
}

Animator.prototype = {
  start: function(finished){
    var startTime = Date.now();
    var duration = this.duration,
        self = this;

    requestAnimationFrame(function step(){
      var p = (Date.now() - startTime) / duration;
      var next =  true;

      if(p < 1.0){
        self.progress(self.easing(p), p);
      }else{
        if(typeof finished === "function"){
          next = finished() === false;
        }else{
          next = finished === false;
        }

        if(!next){
          self.progress(self.easing(1.0), 1.0);
        }else{
          startTime += duration;
          self.progress(self.easing(p), p);
        }
      }

      if(next) requestAnimationFrame(step);
    });
  }
};

在上面的代码里，我们封装出一个简易的动画类 Animator, 这个类的构造器接收三个参数，分别是 duration, process 和 easing。它产生一个对象，包含一个start方法，这个方法用指定 duration、process 和 easing执行动画。

有趣的是，start方法包含一个参数，这个参数是一个布尔类型或者回调函数，当动画结束的时候，如果这个参数是回调函数，将执行这个函数，它的返回值如果不是false那么结束动画，否则循环播放动画。如果这个参数是布尔值flase，那么也循环播放动画。

后续的例子里我们会看到这个类的用法。

连贯的动画

我们尝试使用上面设计的动画类来构造连续播放的动画：

让滑块先向右然后再向下运动

var a1 = new Animator(1000,  function(p){
    var tx = 100 * p;

    block.style.transform = "translateX(" 
      + tx + "px)";     
  });

var a2 = new Animator(1000,  function(p){
  var ty = 100 * p;

  block.style.transform = "translate(100px," 
    + ty + "px)";     
});

block.addEventListener("click", function(){
  a1.start(function(){
    a2.start();
  });
});

在构造更复杂的动画的时候，为了更方便使用，避免回调嵌套，我们可以再实现一个动画队列类：

function AnimationQueue(animators){
  this.animators = animators || [];
}

AnimationQueue.prototype = {
  append: function(){
    var args = [].slice.call(arguments);
    this.animators.push.apply(this.animators, args);
  },
  flush: function(){
    if(this.animators.length){
      var self = this;

      function play(){
        var animator = self.animators.shift();

        if(animator instanceof Animator){
          animator.start(function(){
            if(self.animators.length){
              play();
            }
          });
        }else{
          animator.apply(self);
          if(self.animators.length){
            play();
          }
        }
      }
      play();
    }
  }
};

有了动画队列，我们就可以轻松做更复杂一点的动画，比如：

让滑块沿一个矩形边界运动

var a1 = new Animator(1000,  function(p){
  var tx = 100 * p;
  block.style.transform = "translateX(" 
    + tx + "px)";     
});

var a2 = new Animator(1000,  function(p){
  var ty = 100 * p;
  block.style.transform = "translate(100px," 
    + ty + "px)";     
});

var a3 = new Animator(1000,  function(p){
  var tx = 100 * (1-p);
  block.style.transform = "translate(" 
    + tx + "px, 100px)";     
});

var a4 = new Animator(1000,  function(p){
  var ty = 100 * (1-p);
  block.style.transform = "translateY("  
    + ty + "px)";     
});


block.addEventListener("click", function(){
  var animators = new AnimationQueue();
  animators.append(a1, a2, a3, a4);
  animators.flush();
});

注意到我们的动画队列除了支持Animator对象外，还支持普通的函数，因此我们可以组合起来做一些复杂的运动：

弹跳的小球

var a1 = new Animator(1414,  function(p){
  var ty = 200 * p * p;
  block.style.transform = "translateY(" 
    + ty + "px)";     
});

var a2 = new Animator(1414,  function(p){
  var ty = 200 - 200 * p * (2-p);
  block.style.transform = "translateY(" 
    + ty + "px)";     
});

block.addEventListener("click", function(){
  var animators = new AnimationQueue();
  animators.append(a1,a2, function(){
    this.append(a1, a2, arguments.callee);
  });
  animators.flush();
});

还可以再加入更复杂的效果：

弹跳的小球 - 带阻尼效果

block.addEventListener("click", function(){
  var T = 1414;

  var a1 = new Animator(T,  function(p){
    var s = this.duration * 200 / T;
    var ty = s * (p * p - 1);
    block.style.transform = "translateY(" 
      + ty + "px)";     
  });

  var a2 = new Animator(T,  function(p){
    var s = this.duration * 200 / T;
    var ty = - s * p * (2-p);
    block.style.transform = "translateY(" 
      + ty + "px)";     
  });

var animators = new AnimationQueue();
  function foo(){
    a2.duration *= 0.7;
    if(a2.duration <= 0.0001){
      console.log("done");
      animators.animators.length = 0;
    }
  }
  animators.append(a1 ,foo, a2,
  function b(){
    a1.duration *= 0.7;
    this.append(a1, foo, a2, b);
  });
  animators.flush();
});

有时候我们也需要一些高级的数学技巧：

模拟从圆周甩出小球

$$ x = - r sin(\pi t)$$

$$ y = r - r cos(\pi t)$$

$$ v_x = - \pi r cos(\pi t)$$

$$ v_y = \pi r sin(\pi t)$$

模拟从圆周甩出小球

var a1 = new Animator(2800, function(p){
  var x = -100 * Math.sin(2.8 * Math.PI * p);
  var y = 100 - 100 * Math.cos(2.8 * Math.PI * p);

  block.style.transform = "translate(" + x + "px,"
    + y + "px)";
});

var a2 = new Animator(5000, function(p){
  var x = -100 * Math.sin(2.8 * Math.PI) 
      -100 * Math.cos(2.8 * Math.PI) * Math.PI * 5 * p;

  var y = 100 - 100 * Math.cos(2.8 * Math.PI) 
      + 100 * Math.sin(2.8 * Math.PI) * Math.PI * 5 * p;

  block.style.transform = "translate(" + x + "px,"
    + y + "px)";    
});

block.addEventListener("click", function(){
  a1.start(function(){
    a2.start();
  });
});

小球被甩出的一刻，x、y 轴速度不再变化，小球被甩出前正在做匀速圆周运动，可以求出 $$S_t$$ ，然后再对 $$S_t$$ 求导求出 $$V_t$$

使用贝塞尔曲线

贝塞尔曲线可以用来构造平滑动画。

贝塞尔曲线

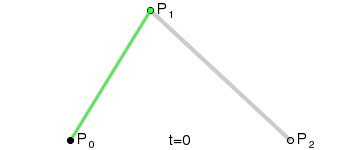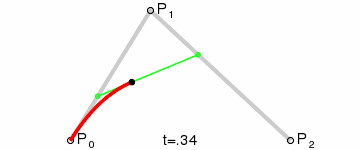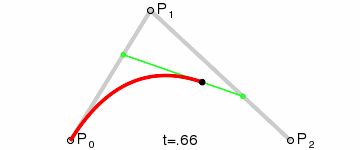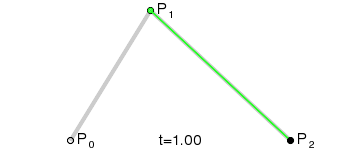
我们可以引入bezier-easing库了来支持贝塞尔曲线的JS动画：

var easing = BezierEasing(0.86, 0, 0.07, 1);
//easeInOutQuint

var a1 = new Animator(2000, function(ep,p){
  var x = 200 * ep;

  block.style.transform = "translateX(" + x + "px)";
}, easing);


block.addEventListener("click", function(){
  a1.start();
});

我们可以通过 cubic-bezier.com 和 easings.net 来定制我们想要的动画效果。

逐帧动画

有时候，我们不但要支持元素的运动，还需要改变元素的外观，比如飞翔的小鸟需要扇动翅膀，这类动画我们可以用逐帧动画来实现:

看上面的代码，其实逐帧动画比之前的动画还要简单，直接用 setInterval 修改元素样式即可，需要注意的是，如果用图片的话，最好是将图片提前预加载了，这样不会出现因为图片还在加载中而显示不出动画的情况。

CSS3 动画

CSS3 支持两种动画，一种是 Transition，一种是 Animation。

Transition 是过渡动画，它只定义在样式的 class 切换的时候发生的动画，因此 Transition 动画相对比较简单，没有循环，也没有事件，它触发的时机只在元素的 className 发生变化的时候。

CSS3 动画支持的浏览器包括：

IE10+
Chrome
Safari

Transition 和 Animation 共同支持的属性：

duration
timing functions
delay

Transition 和 Animation 支持同样的 Timing functions:

linear
ease
ease-in
ease-out
ease-in-out
cubic-bezier(n,n,n,n)

这其实和我们前面的JS动画里的算子概念是一致的，贝塞尔曲线也是一致的：

Transition 圆周运动

<style>
  #block{
    position:absolute;
    left: 200px;
    top: 100px;
    width: 20px;
    height: 20px;
    background: #0c8;
    text-align: center;
    border-radius: 50%;
    transform-origin: 0 100px;
    transform: rotate(0deg);
  }
  #block.play {
    transform: rotate(360deg);
    transition: transform 2.0s linear;
  }
</style>
<div id="block"></div>
block.addEventListener("click", function(){
  block.className = "play";
});

Transition 使用贝塞尔曲线

#block.play {
  transform: translateX(200px);
  transition: transform 2.0s cubic-bezier(0.68, -0.55, 0.265, 1.55);
}

Transition 没有优先级，后面的样式会覆盖掉前面的样式中的某些 Transition 属性，因此当两个 class 都有 Transition 的时候，相互覆盖会导致奇怪的行为：

Transition 样式覆盖

#block.play {
  border-radius: 0;
  transform: scale(2.0);
  background: #c80;
  transition: all 2.0s cubic-bezier(0.68, -0.55, 0.265, 1.55) 3s;
}
#block.play2 {
  /* transition 覆盖*/
  background: #c8f;
  transition: all 2.0s linear 0.5s; 
  transform: scale(2.0) rotate(360deg);
}
block.addEventListener("click", function(){
  block.className = "play play2";
});

Animation 动画支持一些更高级的特性：

keyframes' name
iteration count
direction
animation-fill-mode
webkitAnimationEnd

Animation - 往复圆周运动

#block{
  position:absolute;
  left: 200px;
  top: 100px;
  width: 20px;
  height: 20px;
  background: #0c8;
  text-align: center;
  border-radius: 50%;
  animation: roll 2.0s linear 0s infinite alternate;
  transform-origin: 0 100px;
}
@keyframes roll{
  0%{transform:rotate(0deg)}
  100%{transform:rotate(360deg)}
}

复杂的动画效果可以将 JS 和 CSS3 动画组合使用：

#block{
  position:absolute;
  left: 150px;
  top: 200px;
  width: 20px;
  height: 20px;
  background: #0c8;
  text-align: center;
  border-radius: 50%;
  animation: anim 2.0s linear 0s forwards;
}
@keyframes anim{
  0%{border-radius: 50%}
  50%{border-radius: 0; background: #c80;}
  100%{border-radius: 20%; transform:scale(2.0); background: #08c;}
}

// JavaScript

var easing = BezierEasing(0.68, -0.55, 0.265, 1.55);
var a1 = new Animator(2000, function(ep,p){
  var x = 150 + 200 * ep;
  block.style.left = x + "px";
}, easing);

block.addEventListener("webkitAnimationEnd", function(){
  a1.start();
});

其他内容

特别声明，本文转载于@十年踪迹的《关于动画，你需要知道的》,如果需要转载，烦请注明文章出处：https://www.h5jun.com/post/animations-you-should-know.html

上一篇: React的一些概念 | 下一篇: JavaScript算法练习：Mutations

w3cplus

【转载】关于动画，你需要知道的

简单的 JS 动画

简单动画的问题

动画是“位移”关于“时间”的函数

动画与时间关联

动画时间归一化表示

用时间来控制动画周期精确在1秒

让滑块在2秒内向右匀速移动200px

变速运动

匀加速运动

匀速、匀加速运动对比

匀减速运动

运动的组合

平面上的运动

抛物线运动

正弦线运动

圆周运动

圆周运动 - 参数方程

圆周运动 - 极坐标方程

动画算子： easing

动画的简易封装

动画的简易封装

连贯的动画

模拟从圆周甩出小球

模拟从圆周甩出小球

使用贝塞尔曲线

逐帧动画

CSS3 动画

Transition 圆周运动

Transition 使用贝塞尔曲线

Transition 样式覆盖

Animation - 往复圆周运动

其他内容

关注我们

合作网站

友情链接

关于我们

关于站长

我的作品

w3cplus

你在这里

【转载】关于动画，你需要知道的

简单的 JS 动画

简单动画的问题

动画是“位移”关于“时间”的函数

动画与时间关联

动画时间归一化表示

用时间来控制动画周期精确在1秒

让滑块在2秒内向右匀速移动200px

变速运动

匀加速运动

匀速、匀加速运动对比

匀减速运动

运动的组合

平面上的运动

抛物线运动

正弦线运动

圆周运动

圆周运动 - 参数方程

圆周运动 - 极坐标方程

动画算子： easing

动画的简易封装

动画的简易封装

连贯的动画

模拟从圆周甩出小球

模拟从圆周甩出小球

使用贝塞尔曲线

逐帧动画

CSS3 动画

Transition 圆周运动

Transition 使用贝塞尔曲线

Transition 样式覆盖

Animation - 往复圆周运动

其他内容

关注我们

合作网站

友情链接

关于我们

关于站长

我的作品